I finally found some time to write a short overview article about our latest JMLR paper. It discusses some interesting insights into the dimensionality of your data in a kernel feature space when you only consider the information relevant to your supervised learning problem. The paper also presents a method for estimating this dimensionality for a given kernel and data set.
The overview also contains a few lines of matlab code with which you can have a look at the discussed effect yourself. It all boils down to pictures like these:
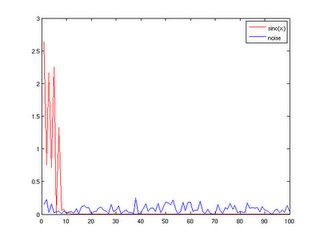
What you see here is the contribution of individual kernel PCA components to the Y samples, divided by the smooth part (red), and the noise (blue), on a toy data set, of course. Kernel PCA components are sorted by decreasing variance. What you can see is that the smooth part is contained in the leading kernel PCA components, while the later components only contain information relevant for the noise. This means that even in infinite-dimensional feature spaces, the actual information is contained in a low-dimensional feature space.
If you are looking for more information, have a look at the overview article, the paper, or a video lecture I gave together with Klaus-Robert Müller in Eindhoven last year. There is also some software available.
Posted by at 2008-11-17 10:06:00 +0100
blog comments powered by Disqus