Scalability has become one of those core concept slash buzzwords of Big Data. It’s all about scaling out, web scale, and so on. In principle, the idea is to be able to take one piece of code and then throw any number of computers at it to make it fast.
The terms “scalable” and “large scale” have been used in machine learning circles long before there was Big Data. There had always been certain problems which lead to a large amount of data, for example in bioinformatics, or when dealing with large number of text documents. So finding learning algorithms, or more generally data analysis algorithms which can deal with a very large set of data was always a relevant question.
Interestingly, this issue of scalability were seldom solved using actual scaling in in machine learning, at least not in the Big Data kind of sense. Part of the reason is certainly that multicore processors didn’t yet exist at the scale they do today and that the idea of “just scaling out” wasn’t as pervasive as it is today.
Instead, “scalable” machine learning is almost always based on finding more efficient algorithms, and most often, approximations to the original algorithm which can be computed much more efficiently.
To illustrate this, let’s search for NIPS papers (the annual Advances in Neural Information Processing Systems, short NIPS, conference is one of the big ML community meetings) for papers which have the term “scalable” in the title.
Here are some examples:
-
Scalable Inference for Logistic-Normal Topic Models
… This paper presents a partially collapsed Gibbs sampling algorithm that approaches the provably correct distribution by exploring the ideas of data augmentation …
Partially collapsed Gibbs sampling is a kind of estimation algorithm for certain graphical models.
-
A Scalable Approach to Probabilistic Latent Space Inference of Large-Scale Networks
… With […] an efficient stochastic variational inference algorithm, we are able to analyze real networks with over a million vertices […] on a single machine in a matter of hours …
Stochastic variational inference algorithm is both an approximation and an estimation algorithm.
-
Scalable kernels for graphs with continuous attributes
… In this paper, we present a class of path kernels with computational complexity $O(n^2(m + \delta^2 ))$ …
And this algorithm has squared runtime in the number of data points, so wouldn’t even scale out well even if you could.
Usually, even if there is potential for scalability, it usually something that is “embarassingly parallel” (yep, that’s a technical term), meaning that it’s something like a summation which can be parallelized very easily. Still, the actual “scalability” comes from the algorithmic side.
So how do scalable ML algorithms look like? A typical example are the stochastic gradient descent (SGD) class of algorithms. These algorithms can be used, for example, to train classifiers like linear SVMs or logistic regression. One data point is considered at each iteration. The prediction error on that point is computed and then the gradient is taken with respect to the model parameters, giving information about how to adapt these parameters slightly to make the error smaller.
Vowpal Wabbit is one program based on this approach and it has a nice definition of what it considers to mean scalable in machine learning:
There are two ways to have a fast learning algorithm: (a) start with a slow algorithm and speed it up, or (b) build an intrinsically fast learning algorithm. This project is about approach (b), and it’s reached a state where it may be useful to others as a platform for research and experimentation.
So “scalable” means having a learning algorithm which can deal with any amount of data, without consuming ever growing amounts of resources like memory. For SGD type algorithms this is the case, because all you need to store are the model parameters, usually a few ten to hundred thousand double precision floating point value, so maybe a few megabytes in total. The main problem to speed this kind of computation up is how to stream the data by fast enough.
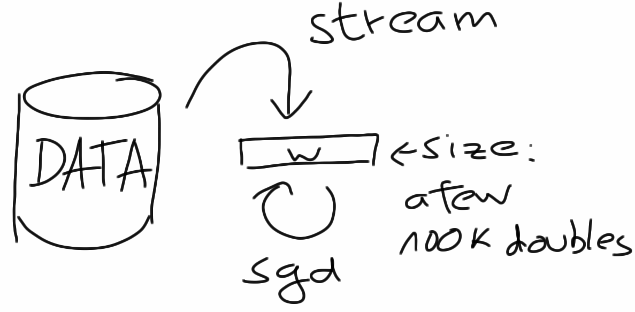
To put it differently, not only does this kind of scalability not rely on scaling out, it’s actually not even necessary or possible to scale the computation out because the main state of the computation easily fits into main memory and computations on it cannot be distributed easily.
I know that gradient descent is often taken as an example for map reduce and other approaches like in this paper on the architecture of Spark, but that paper discusses a version of gradient descent where you are not taking one point at a time, but aggregate the gradient information for the whole data set before making the update to the model parameters. While this can be easily parallelized, it does not perform well in practice because the gradient information tends to average out when computed over the whole data set.
If you want to know more, this large scale learning challenge Sören Sonnneburg organized in 2008 still has valuable information on how to deal with massive data sets.
Of course, there are things which can be easily scaled well using Hadoop or Spark, in particular any kind of data preprocessing or feature extraction where you need to apply the same operation to each data point in your data set. Another area where parallelization is easy and useful is when you are using cross validation to do model selection where you usually have to train a large number of models for different parameter sets to find the combination which performs best. Again, even here there is more potential for even speeding up such computations using better algorithms like in this paper of mine.
I’ve just scratched the surface of this, but I hope you got the idea that scalability can mean quite different things. In Big Data (meaning the infrastructure side of it) what you want to compute is pretty well defined, for example some kind of aggregate over your data set, so you’re left with the question of how to parallelize that computation well. In machine learning, you have much more freedom because data is noisy and there’s always some freedom in how you model your data, so you can often get away with computing some variation of what you originally wanted to do and still perform well. Often, this allows you to speed up your computations significantly by decoupling computations. Parallelization is important, too, but alone it won’t get you very far.
Luckily, there are projects like Spark and Stratosphere/Flink which work on providing more useful abstractions beyond map and reduce to make the last part easier for data scientists, but you won’t get rid of the algorithmic design part any time soon.
Posted by Mikio L. Braun at 2014-07-02 17:38:00 +0000
Three books on large scale learning
Actually, scalability isn't (yet) a standard topic in machine learning. There are some algorithms which are known to scale well. In any case Mining of Massive Datasets is a nice overview of techniques to deal with large data sets without getting too technical. You can also download the PDF for free from the authors.. Large-Scale Kernel Machines is a much more advanced book highlighting some of the approaches discussed here, but this is definitely more a graduate studies level of textbook. Finally, Scaling up Machine Learning looks very interesting. I haven't read it so far, but it explicitly deals with the parallelization aspect of it, and the main author of Vowpal Wabbit, John Langford, is one of the editors. Again, I think this is a pretty advanced textbook.
Be advised, these are all affiliate links which take you to Amazon. This also means that you don't see the pictures if you have ad block activated. You may safely whitelist my site, I don't plan on having ad banners any time soon.