jblas: 1.1 Released and Some Examples
I have just released jblas 1.1 (release notes). The main addition are Singular Value Decomposition (both “full” and “sparse”), and fixing a nasty bug with complex return values. Basically, the way complex return values are treated by g77 and gfortran are drastically different leading to some very odd bugs resulting from a confused stack frame.
Unfortunately, I also had to remove support for 32-bit Mac OS X in the precompiled jar file. The reason is that I lost access to the 32-bit machine I originally used to compile ATLAS for Mac, and any other machine I got my hands on is apparently running with 64-bits. Also, I didn’t quite get the 32-bit version of gcc working. But in case you have a 32-bit machine and need jblas, please contact me and I’ll help you compile the beast.
Examples
To make up for that, here are two examples of how to use jblas. These are from my poster at this years MLOSS workshop at ICML.
You can download the slides here.
I’ve also put the source up on github. Note that these sources are not meant to be a good example for coding style or project layout, but just an example of how to use jblas!
Please take a few seconds for jsMath do its magic… .
Kernel Ridge Regression
The first example is taken from machine learning. Let’s implement the following: Noisy sinc data set learned with Kernel Ridge Regression (KRR) with a Gaussian kernel.
The data set
First, we define the sinc function, which is usually defined as follows (up to scaling of the $x$): \(\text{sinc}(x) = \sin(x) / x \text{ if } x \neq 0 \text{ and } 1 \text{ if } x = 0.\)
The first try to code this in Java using jblas is to just focus on the part where $x \neq 0$:
DoubleMatrix sinc(DoubleMatrix x) {
return sin(x).div(x);
}Note how sin and div “vectorize” over a number of vectors given as
a matrix.
Now let’s add the $x=0$ case. Since the code like this:
DoubleMatrix safeSinc(DoubleMatrix x) {
DoubleMatrix xIsZero = x.eq(0);
return sin(x).div(x.add(xIsZero)).add(xIsZero);
}Note how we first “patch” for the case where x is zero, and then again add those points to get the required output.
Next, we draw some data from the sinc function and add noise. Our data model looks like this: \(X \sim \text{uniformly from -4, 4}\) \(Y = \text{sinc}(x) + \sigma_\varepsilon^2 \varepsilon\) \(\varepsilon \sim \mathcal{N}(0, 1).\)
The following function generates a data set by returning an array of two DoubleMatrices representing $X$ and $Y$.
DoubleMatrix[] sincDataset(int n, double noise) {
DoubleMatrix X = rand(n).mul(8).sub(4);
DoubleMatrix Y = sinc(X) .add( randn(n).mul(noise) );
return new DoubleMatrix[] {X, Y};
}The Gaussian kernel
For KRR, we need to compute the whole kernel matrix. The kernel function is defined as \(k(x,z) = \exp\left( - \frac{||x - z||^2}{w} \right)\)
You can easily compute the kernel matrix using Geometry.pairwiseSquaredDistances().
DoubleMatrix gaussianKernel(double w,
DoubleMatrix X,
DoubleMatrix Z) {
DoubleMatrix d =
Geometry.pairwiseSquaredDistances(X.transpose(),
Z.transpose());
return exp(d.div(w).neg());
}Kernel Ridge Regression
KRR learns a “normal” kernel model of the form \(f(x) = \sum_{i=1}^n k(x, X_i)\alpha_i\) with \(\alpha = (K + \lambda I)^{-1} Y,\) where $K$ is the kernel matrix \(K_{ij} = k(X_i, X_j).\)
With jblas, you would compute the $\alpha$ as follows:
DoubleMatrix learnKRR(DoubleMatrix X, DoubleMatrix Y,
double w, double lambda) {
int n = X.rows;
DoubleMatrix K = gaussianKernel(w, X, X);
K.addi(eye(n).muli(lambda));
DoubleMatrix alpha = Solve.solveSymmetric(K, Y);
return alpha;
}
DoubleMatrix predictKRR(DoubleMatrix XE, DoubleMatrix X,
double w, DoubleMatrix alpha) {
DoubleMatrix K = gaussianKernel(w, XE, X);
return K.mmul(alpha);
}The function predictKRR computes predictions on new points stored as
rows of the matrix XE.
Computing the mean-squared error
Finally, in order to compute the error of our fit, we would like to compute the mean-squared error. \(\frac 1n\sum_{i=1}^n (Y_i - Y'_i)^2.\)
In jblas:
double mse(DoubleMatrix Y1, DoubleMatrix Y2) {
DoubleMatrix diff = Y1.sub(Y2);
return pow(diff, 2).mean();
}Conjugate Gradients
As a second example, let’s implement the conjugate gradients algorithm. This is an iterative algorithm for solving linear equations of the form $Ax = b$, where $A$ is symmetric and positive definite.
The pseudo-code looks as follows:
- $r \gets b - Ax$
- $p \gets r$
- repeat
- $\alpha \gets \frac{r^Tr}{p^T A p}$
- $x \gets x + \alpha p$
- $r’ \gets r - \alpha A p$
- if $r’$ is sufficiently small, exit loop
- $\beta \gets \frac{ {r’ }^T r’}{r^Tr}$
- $p \gets r + \beta p$
- $r \gets r’$
- end repeat
In jblas, the algorithm looks as follows (numbers in comments indicate steps in the algorithm above.)
DoubleMatrix cg(DoubleMatrix A, DoubleMatrix b,
DoubleMatrix x, double thresh) {
int n = x.length;
DoubleMatrix r = b.sub(A.mmul(x)); // 1
DoubleMatrix p = r.dup(); // 2
double alpha = 0, beta = 0;
DoubleMatrix r2 = zeros(n), Ap = zeros(n);
while (true) { // 3
A.mmuli(p, Ap);
alpha = r.dot(r) / p.dot(Ap); // 4
x.addi(p.mul(alpha)); // 5
r.subi(Ap.mul(alpha), r2); // 6
double error = r2.norm2(); // 7
System.out.printf("Residual error = %f\n", error);
if (error < thresh)
break;
beta = r2.dot(r2) / r.dot(r); // 8
r2.addi(p.mul(beta), p); // 9
DoubleMatrix temp = r; // 10
r = r2;
r2 = temp;
}
return x;
}For better speed, I have tried to reduce the number of matrix
allocations and used the in-place variants of the arithmetic
operations where possible. These kinds of tweaks can often give some
performance boost. For example, Ap is used to hold the result of
$Ap$, and so on.
As a side-effect the assigment $r \gets r’$ actually becomes a swap
between the matrices stored in r and r2.
Some Tips On Using Cassandra
Also see this follow-up post.
The last few months we have been working on migrating our main database for twimpact to Cassandra. When we first started using Cassandra, using the default configuration we quickly ran into all kinds of performance and stability issues. For example, Cassandra would consume huge amounts of memory and at some point do nothing else than garbage collections. Or, Cassandra requests would time out again and again.
It turns out that Cassandra, like any sufficiently complex piece of software, requires proper configuration and usage. In this post, I try to summarize some basic facts about Cassandra and our experience with configuring it properly. The post is a bit longer, so here are the main points first:
- Monitor Cassandra for memory consumption and stage throughput.
- Set your Memtable thresholds low.
- Access Cassandra concurrently.
- Don’t store all your data in a single row.
- Beware of time-outs.
Small architecture overview of Cassandra
OK, here is the absolute minimum you need to know to understand what I’m talking about. Note that I’ll only discuss single node configurations. With clustering, it becomes somewhat more complex.
-
Cassandra basic unit of storage is a column family which is like a hash of hashes. Put differently, you get a keyed index into objects stored as hashes.
-
Cassandra writes are first written to an on-disk commit log (in case the server crashes), and then written to in-memory Memtables. If these get full, they are flushed to on-disk SSTables (which are immutable). Background threads then perform garbage collection and compaction on these SSTables.
-
Cassandra is written following the SEDA principle. This means that Cassandra basically is a collection of independent modules called stages which communicate through message queues. These modules can dynamically adapt their workload by either adjusting the number of worker threads or by throttling their operation. The most important stages are ROW-MUTATION-STAGE (which takes care of writes) and READ-ROW-STAGE (doing reads). See also this blog post for more detailed information.
-
Cassandra is configured through the file
conf/storage-conf.xmlrelative to where Cassandra is started.
Monitoring Cassandra
The standard tools for monitoring Java processes also apply to Cassandra, including jvisualvm and jconsole which are included in Sun’s^H^H^H^HOracle’s, SDK.
Cassandra also exposes a number of management beans (see the tab “MBeans” in jconsole). The interesting ones are:
-
org.apache.cassandra.service.StorageServicehas statistics about read and write latencies. -
In
org.apache.cassandra.db.ColumnFamilyStoresyou find beans for each column family where you can see how many bytes they are using, how many SSTables exist (the on-disk storage). -
Under org.apache.cassandra.concurrent, you can see the individual stages in the Cassandra server.
You can also get a quick overview of the stages with the nodetool
command. Let’s say Cassandra is running on 127.0.0.1, then you type
bin/nodetool -host 127.0.0.1 tpstats and get an overview over all
stages and how many active and pending jobs you have.
If everything is running okay, you will normally see a 0 or 1 in the Active and Pending column, and a really huge number in the Completed column. If one of the stages (in particular the ROW-READ-STAGE) has a large number of pending jobs, then something is amiss (see below).
Set low Memtable thresholds
*Update*: As some commentors pointed out, the following paragraph is misleading with respect to the different kinds of garbage collection. The parallel garbage-collector is actually a stop-the-world garbage collector working on the so-called “young generation”. The term “parallel” refers to it being implemented in a multi-threaded fashion for better speed. The ConcurrentMarkSweep GC is a “Full GC”, but apart from the initial mark and the final cleanup phase, it is really concurrent, meaning that it runs in parallel to the normal process.
What remains true is that Cassandra probably needs a lot more memory than a back-of-the-envelope computation based on the Memtable sizes would suggest. But it is not a problem to have it run in a stable manner. For more information, see the follow-up blog post.
Probably the most important configuration options are the thresholds
which control when Memtables are flushed. Here is a list of the
options: (The Cassandra Wiki is not up-to-date with the
names. MemtableSizeInMB became MemtableThroughputInMB in 0.6)
| MemtableThroughputInMB | How many megabytes of data to store before flushing |
| BinaryMemtableThroughputInMB | The same for a special kind of Memtable (haven't met those one yet) |
| MemtableOperationsInMillions | How many operations on Memtable before flushing |
| MemtableFlushAfterMinutes | How many minutes to wait before flushing |
All these parameters apply per column family.
Now, you might think, if you have ten column families and MemtableThroughputInMB is 128 (the default!), then you will need about 1.3 GB of RAM. However, for reasons not totally clear to me, Cassandra will use up a lot more RAM. In our twimpact installation we currently have 12 column families. If I set the limit to 1MB for each column family, Cassandra needs at least 512MB. On our main database, I’ve currently set the limits to 16MB and after some burn-in time, Cassandra happily expands to first 10GB, then the whole 16GB allotted.
You should closely monitor the memory consumption using a tool like jconsole. Cassandra’s performance will be much worse if you don’t give it enough RAM as it will at some point start to do mostly garbage collection. In particular, you have to watch out for the ConcurrentMarkSweep GCs. Cassandra is configured to use a parallel garbage collector which has two kinds of collection: ParNew runs totally in parallel to other threads and collects small amounts of data. If that does not suffice, the JVM performs a full GC with ConcurrentMarkSweep which takes much longer.
Here is a screenshot of our Cassandra process after running for about a day. This behavior should be considered “normal”. In particular, the JVM hasn’t feel forced to do a full GC so far.
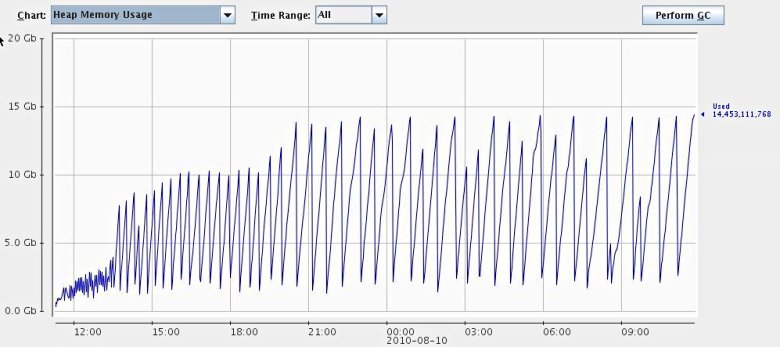
I’ve searched the code a bit and done some profiling with jvisualvm, but I haven’t been able to really understand what is going on. Apparently, all the data is contained in Memtables, but normally this data should be freed once the Memtable is flushed. Cassandra is using soft references to trigger deletion of some files, and I’ve seen soft references leading to drastically different memory behavior (read: more memory), but I’m not sure this is really the case here. There is also a bug report which seems to address a similar problem. Restarts also help, but are certainly out of question in production.
In summary, for now give Cassandra a lot of RAM and everything should be OK.
Cassandra loves concurrency
Cassandra really loves concurrent access. You can get at least a four fold increase of throughput if you access Cassandra from four to eight threads at the same time.
For twimpact, it was actually a bit hard to turn the analysis multi-threaded because we need to update a lot of statistics and there is no provision for locking in Cassandra, but it certainly was worth it.
One thing to remember, though, is to adjust the two configuration
options ConcurrentReads and ConcurrentWrites accordingly. These
two directly set the number of worker threads for the ROW-READ-STAGE
and the ROW-MUTATION-STAGE, meaning that these aren’t adjusted
automatically. It probably makes sense to have at least as many
threads as you expect to use. However, as we’ll discuss next, reads
can take a long time, so it’s probably safe to have enough threads
there.
Don’t store all your data in a single row
One operation where Cassandra isn’t particularly fast is when you store all your data in a single row (i.e. under a single key). Since the columns are automatically sorted, single rows are useful to store indices, or other kinds of sorted lists. But you should be careful not to store several hundred thousand objects in there, otherwise reads and writes will get pretty slow (I’m talking about several seconds here, not milliseconds).
In our case, tweetmeme was such a case
since they apparently have many different messages retweeted (even
more than justinbieber, our other
gold standard when it comes to excessive number of retweets ;)).
Beware of timeouts
Depending on the client you are using, there might be some timeouts on
the sockets (which is generally a good thing). In addition there is
also the configuration parameter RpcTimeoutInMillis, which is an
internal timeout for requests.
Be careful not to set those parameters too low, I recommend 30 seconds or longer. Reads can take up to several seconds (see above) if you accidentally have really large rows. The problem is that unlike network problems, the request will time out on each retry, and your application will basically hang.
Summary
In summary, I think Cassandra is a very interesting project. They certainly have the right combination of technology in there: Dynamo’s fully distributed design, Bigtable’s main storage principles, robustness to failures. In our second reanalysis run, we’re getting still about 290 tweet/s analyzed with already 50 million in the database (remember that each tweet analysis involves about 15-20 operations with read/write ratio of about 1:2). On the other hand, getting there probably requires a bit more configuration and monitoring than for more mature databases.
A Rejected Paper Is Not The End
Now that the preliminary NIPS reviews have been out, it is time to remember that a rejected paper is not the end. In particular if you’re a beginning graduate student and you’ve submitted your first paper, be advised that you need to keep on working on your paper, and the worst that can happen is if you let yourself be discouraged and just discard the hours of work you’ve put into your paper by stopping to work on it.
First, you need to understand that there are many different reasons why your paper was rejected.
-
NIPS reviewers are usually heavily overloaded. A NIPS reviewer is typically asked to review about eight papers. Given the already high workload, this means that you end up reviewing eight papers in two to three days. So if your paper is less than clear, or the idea doesn’t easily fit in one of the existing frameworks, chances are high that the reviewer does not “get it”, and plays it safe by rejecting your paper.
-
Often, reviewers offload some of the papers to their graduate students and Post-Docs which are sometimes not yet experienced enough adopt a high-level view of your paper and to give a faithful evaluation of the merits of your paper.
-
At a competitive conference such as NIPS, one lukewarm review is enough to get your paper rejected. So a single reviewer can get your paper rejected.
-
Finally, chances are high that while your approach and idea have sufficient merit, you failed on some of the other aspects. For example, you haven’t sufficiently put your work into the context of the existing body of work, or your experimental evaluation was faulty.
Almost no paper is accepted in its first submission. Everyone has some war stories about papers which were accepted only after several submissions, after switching journals, complete rewrites and appealing to the action editor. Each reject, even if the reviews are completely off the mark, is an important feedback on how your work is perceived and gives you hints on how to improve your paper.
In summary, a reject is not the end, in fact, it is only the beginning:
-
If possible, you can write a rebuttal, clearing up misunderstandings. In my experience, however, this has seldom led to an improvement of scores.
-
Resubmit an improved version to another conference. The advantage of a conference is a somewhat predictable review schedule. The disadvantage is that you will usually get new reviewers with the danger that one of them will again not like your paper.
-
Resubmit your paper to a workshop. Workshops usually have much lower thresholds and also don’t lead to a “real” publication, but they allow you to present your work to others and get feedback, and someone in your audience might be your next reviewer.
-
Resubmit to a journal. This might require to improve your paper a lot. The main advantage of journals is that the review process has several rounds. After a reject, you typically are assigned to the same reviewers, meaning that you can actually work with the reviewer to improve your paper to the point where it will be accepted.