Threads, Exceptions, Net::HTTP, Timeouts and JRuby
I recently had some fun debugging a little application of mine written in JRuby which crawls the twitter search API looking for specific tweets. The problem was, every now and again, the crawler would hang even if I set appropriate timeouts. The crawler consisted of two threads, one periodically issuing a search to twitter, and another one writing the results into the database.
The first surprise to me was that in Ruby, by default, if there is an
exception in a thread, the thread silently dies, not even issuing an
error message. Only after you joined the thread, you get the error
message. You can set Thread.abort_on_exception = true which completely
kills your application, however. This meant that what appeared to be
missed timeouts could just as well be uncaught exceptions.
So when working with multithreaded applications, enclosing the whole
thread in a begin .. rescue Exception => e ... end is important if you
want to get noticed about errors at all.
But still, the thread would misteriously die without properly handling the timeout. Some digging deeper revealed an old bug report and an interesting article about Ruby and timeouts in general which seemed to imply that timeouts might not always work, in particular if system calls are involved. It was unsure, though, whether the situation is the same for JRuby which uses native threads instead of Green threads (simulated threads by doing explicit time-slicing in the interpreter).
So I started to read the JRuby
sources, to understand
where and how timeouts are implemented in Net::HTTP. Which lead to my
next surprise: Net::HTTP completely handles timeouts through the
Timeout module, not on a socket level. It does not use the
possibilities to set timeouts on reads or writes but encapsulates all
the significant portions of code in Timeout::timeout { ... } calls. I
also found a nice old post by Charles Nutter (a.k.a. headius)
explaining the implementation in depth.
I guess based on that post, JRuby has started to implement Timeout again in Java (source). And some first tests revealed that this timeout plays well within Net::HTTP, but my crawler was still hanging every once and again.
Finally, I found the last missing piece of information: From the sources, it seems that JRuby’s implementation of the Timeout module raises the Timeout::ExitException when the timeout happened. However, that is a ruby 1.9 feature, in ruby 1.8, the exception was named Timeout::Error. So basically, I was catching the wrong exception, in fact not catching it at all, thereby killing the thread (silently). Interestingly, some more testing showed that if JRuby raises a Timeout::Error if you use the Timeout module yourself, but raises a Timeout::ExitException when you’re using Net::HTTP.
In the end, I just enclose the whole HTTP request section with a Timeout::timeout of my own, catching both Timeout::Error and Timeout::ExitException and finally everything was running robustly.
So in summary
- Uncaught exceptions silently kill threads in ruby.
- Net::HTTP does it’s own timeouts through the Timeout module.
- Somtimes, JRuby raises Timeout::ExitException, not Timeout::Error. Will be fixed in JRuby 1.4 (see below)
I guess I should post a bug report on the latter… .
Update: I submitted a bug report, and it’s already fixed! Those jruby people are really incredibly fast!
Machine Learning Twibe
Twibes is some new twitter-related website which manages topic-related groups of people and collects tweets based on up to three tags.
Since apparently nobody did so far, I set up a twibe on machine learning. Follow the link and click on “Join” on the right and side to join.
Currently, the group is picking up tweets with either “machine learning”, “#machlearn”, or “#machine-learning” in them. Anyone got an idea how to improve the tags?
Some Benchmark Numbers for jblas
The last few days I’ve been putting together a benchmarking tool for jblas which I’ll hope to release to the public as soon as I’ve figured out how to best package that beast.
It compares my own matrix library, jblas against the Matrix Toolbox for Java, Colt, as well as simple implementations in C and Java, and, of course, ATLAS.
All experiments were run on my Laptop which sports an Intel Core 2 CPU (T7200) with 2GHz. Maybe the most remarkable feature of this CPU (and many other Intel CPUs as well) is the rather large 2nd level cache of 4MB which will come in handy as we’ll see below.
Some more information on the plots: C+ATLAS amounts to taking C for vector addition and ATLAS for matrix vector and matrix matrix multiplication. Shown is the number of theoretical floating point operations. For example, adding two vectors with n elements requires n additions, multiplying a matrix with n squared elements requires 2n^2 additions and multiplications. Now I know that there exist matrix multiplication algorithm which require less than cubic number of operations, but I’ve just sticked to the “naive” number of operations as that is what ATLAS implements, as far as I know.
Vector Addition
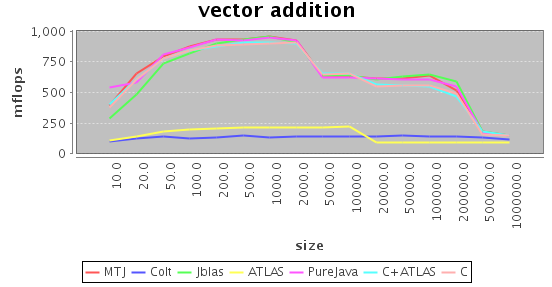
In vector addition the task is simply to add all elements of one vector to all elements of the other vector (in-place). What is interesting about vector addition is that there is really little you can do to optimize the flow of information: You just have to go through the whole vector once. Basically, all methods are on par, with the exception of Colt and ATLAS (!!). No idea what they did wrong, though.
You can also very nicely see the L1 and L2 cache edges resulting in the two steps. On CPUs with smaller L2 cache (like, for example, most AMD CPUs), the shoulder is much less pronounced.
Matrix-Vector Multiplication
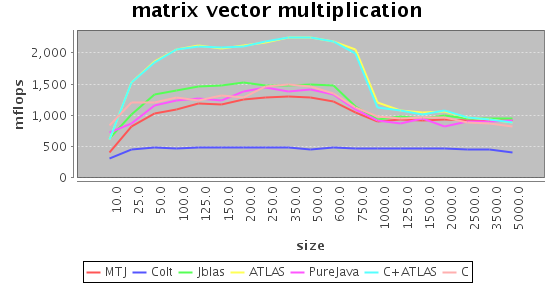
Matrix-vector multiplication can be thought of as adding up the columns of a matrix given the weights of the vector. Similar to vector addition, you basically have to go through the whole data once, there is little you can do about it. However, if you are clever, you can make at least sure that the input and output vectors stay in cache which leads to a better throughput.
Here, ATLAS is faster than the naive implementations by roughly 50%. jblas also uses a naive implementation. The reason is that Java needs to copy an array when you pass it to native code, and since you basically have to go through the matrix once, you loose more time copying the matrix than simply doing the computation in Java itself.
Matrix-Matrix Multiplication
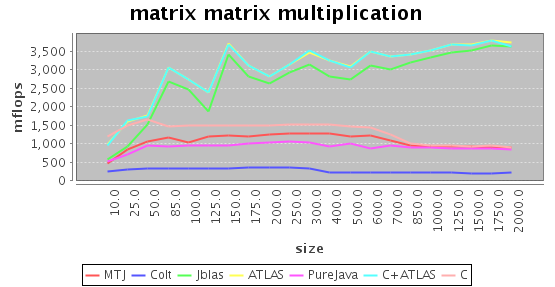
In matrix-matrix multiplication the ratio of memory movements to operations is so good that you can practically reach the theoretical maximum throughput on modern memory architectures - if you arrange your operations accordingly. ATLAS really outshines the other implementations here, getting to almost two (double precision!) floating point operations per clock cycle.
Luckily, copying the n squared many floats can be asymptotically neglected compared to the n cube many operations meaning that it pays of to use ATLAS from Java. The performance of jblas is very close to ATLAS, and becomes even closer for large matrices.
Summary
On the buttom line, I’m glad that jblas is pretty fast, certainly faster than Colt and on par with MTJ except for matrix-matrix multiplication. I should add that I used the Java-only versions of Colt and MTJ. It should be possible to optionally link against the ATLAS versions, although Colt does not integrate these methods as well as jblas, and I’m not sure whether MTJ does that.
Also, in my opinion jblas is easier to use because it only uses one matrix type, not distinct types for vectors and matrices. I’ve tried that at first, too, but then often ended up in situations where a computation results in a row or column vector which I then had to artificially cast to a vector so that I could go on.
Of course, MTJ and Colt are currently more feature rich, supporting, for example, sparse matrices or banded storage schemes, but if you want to have something simple which performs well right now, why not take jblas ;)